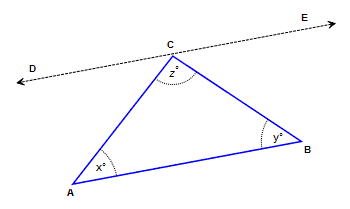
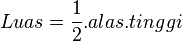SUDUT
PENGERTIAN SUDUT
Sudut dalam
geometri adalah besaran
rotasi
suatu ruas garis dari satu titik pangkalnya ke posisi yang lain. Selain
itu, dalam bangun dua dimensi yang beraturan, sudut dapat pula
diartikan sebagai
ruang antara dua buah ruas
garis lurus yang saling
berpotongan.
Bagian – bagian sudut :
1. Kaki sudut, sinar garis yang membentuk suatu sudut
2. Titik sudut, titik potong pangkal sinar dari kaki sudut
3. Daerah sudut, daerah yang terbentuk antara dua kaki sudut
Jenis – jenis Sudut
1. Sudut siku-siku, yaitu sudut yang besarnya 90⁰.
2. Sudut lancip, yaitu sudut yang besarnya antara 0 ⁰ dan 90 ⁰ atau 0 ⁰ < D < 90 ⁰,
3. Sudut tumpul, yaitu sudut yang besarnya di antara 90 ⁰ dan 180 ⁰ atau 90 ⁰ < D < 180 ⁰.
4. Sudut lurus, yaitu sudut yang besarnya 180 ⁰.
5. Sudut refleks, yaitu sudut yang besarnya antara 180 ⁰ dan 360 ⁰, atau 180 ⁰ < D < 360 ⁰.
Hubungan antar sudut
1. Sudut yang saling berpenyiku, dua sudut yang jumlah ukurannya 90 : ∠ ABD + ∠ DBC = 90
Jika dua buah sudut membentuk sudut siku-siku (90 ⁰), maka sudut yang satu merupakan penyiku sudut yang lain dan kedua sudut itu dikatakan saling berpenyiku.(berkomplemen)
2. Sudut yang saling berpelurus, dua sudut yang jumlah ukurannya 180 : ∠ PQS + ∠ SQT + ∠ TQR = 180
Jika dua buah sudut membentuk sudut lurus, maka sudut yang satu merupakan pelurus sudut yang lain dan kedua sudut itu dikatakan saling berpelurus (bersuplemen).
HUBUNGAN ANTAR SUDUT JIKA DUA GARIS SEJAJAR DIPOTONG OLEH GARIS LAIN
1. Sudut sehadap, besarnya sama. Yakni ∠1 = ∠5, ∠2 = ∠6, ∠4 = ∠8, ∠3 = ∠7.
2. Sudut dalam berseberangan, besarnya sama. Yakni ∠3 = ∠5, ∠4 = ∠6
3. Sudut luar berseberangan, besarnya sama. Yakni ∠1 = ∠7, ∠2 = ∠8
4. Sudut dalam sepihak, jumlah keduanya adalah 180o. Yakni ∠4 + ∠5 = 180, ∠3 + ∠6 = 180.
5. Sudut luar sepihak, jumlah keduanya adalah 180o. Yakni ∠2 + ∠7 = 180, ∠1 + ∠8 = 180.
6. Sudut bertolak belakang, besarnya sama. Yakni ∠1 = ∠3, ∠2 = ∠4, ∠5 = ∠7, ∠6 = ∠8.
MENGENAL SATUAN SUDUT
Ukuran sudut dalam derajat
1 derajat adalah besar sudut yang diputar oleh jari-jari lingkaran sejauh 1/360 putaran atau 1° = 1/360 putaran
Ukuran sudut yang lebih kecil daripada derajat adalah menit (‘) dan detik (“)
Hubungan antara derajat, menit, dan detik dapat dinyatakan sebagai berikut :
1 derajat = 60 menit atau 1° = 60’
1 menit = 1/60 derajat atau 1’ = 1/60°
1 menit = 60 detik atau 1’ = 60”
1 detik = 1/60 menit atau 1” = 1/60’
Ukuran sudut dalam radian
1 radian sama dengan besar sudut pusat lingkaran yang dibatasi oleh busur lingkaran yang panjangnya sama dengan jari-jari
1° = p/180 radian atau 1 radian = 180°/p
Jika nilai p = 3,14159 maka hubungannya dapat juga dinyatakan :
1° = p/180 radian = 3,14159/180 = 0,017453 atau
1 radian = 180°/p = 180°/3,14159 = 57,296°
. Berikut ini langkah-langkahnya.
- Lukislah sinar garis BC, yang akan menjadi kaki sudut dari sudut ABC.
- Dengan menggunakan jangka, buatlah busur lingkaran yang berpusat di titik B sedemikian sehingga memotong sinar garis BC.
- Dengan pengaturan jangka yang sama (jari-jari yang sama), buatlah
juga busur lingkaran yang berpusat di titik perpotongan antara sinar
garis BC dan busur lingkaran yang terbentuk pada langkah 2,
sehingga busur tersebut berpotongan dengan busur berpotongan dengan
busur pada langkah 2 tersebut.
- Namailah titik potong kedua busur dengan A. Kemudian hubungkan titik B dan A untuk melukis sinar garis BA. Sudut ABC besarnya 60°.

Melukis Sudut yang Besarnya 30°
Secara jelas, sudut yang besarnya 30° merupakan sudut yang besarnya
setengah dari sudut 60°. Sehingga, sudut 30° dapat dilukis dengan membagi sudut 60° menjadi 2 bagian yang sama besar.

Dari ilustrasi di atas, kita juga dapat menyimpulkan bahwa sudut ABD besarnya 30°.
Melukis Sudut yang Besarnya 45°
Sudut 45° dapat dilukis dengan membagi sudut 90° menjadi 2 bagian
yang sama besar. Padahal, melukis sudut 90° hampir sama dengan
melukis segitiga siku-siku. Perhatikan ilustrasi dalam melukis sudut
KLM yang besarnya 45° berikut.

MEMBUAT SUDUT BARU DENGAN UKURAN YANG SAMA DENGAN SUDUT YANG DIKETAHUI
Dengan menggunakan jangka dan penggaris lukislah sudut yang ukurannya sama dengan sudut A berikut

1. Gambarlah sebuah sinar yang berpangkal di E dengan menggunakan penggaris!
2. Buatlah busur dengan pusat A dengan
menggunakan jangka sedemikian hingga sehingga memotong kaki-kaki sudut
tersebut. Berilah nama titik-titik potongnya titik B dan C!
3. Dengan menggunakan jangka, buatlah
busur dengan pusat E dan berjari-jari sama dengan nomor 2 di atas
sehingga memotong sinar yang berpangkal di E. Berilah nama titik
potongnya titik F!
4. Buatlah busur dengan pusat F dan
berjari-jari BC sehingga memotong busur yang telah dibuat pada langkah
3. Berilah nama titik potongnya titik D!
5. Gambarlah sinar ED dengan menggunakan penggaris!
CARA MEMBAGI DUA SUDUT SAMA BESAR
Adapun cara membaginya adalah sebagai berikut.
a. Jangkakan dari A dengan ukuran tertentu sehingga membuat busur DE seperti Gambar (a).
 |
| r |
b. Jangkakan dari D dengan ukuran tertentu dan juga dari E kedua busur hasil penjangkaan berpotongan di
F seperti Gambar (b).
c. Hubungkan A dan F. Garis AF membagi sudut BAF dan ∠CAF sama besar seperti Gambar (c).
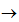 B dan g : B
B dan g : B 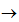 C. Jika h adalah fungsi komposisi dari f atau g .
C. Jika h adalah fungsi komposisi dari f atau g .  dengan
dengan B dan g : B
B dan g : B  C. Jika h adalah fungsi komposisi dari f atau g .
C. Jika h adalah fungsi komposisi dari f atau g .